SURFACES IN SPACE

Week 4

In my Math 240 class, I studied the subject of “Surfaces in Space” during this week. It is about drawing an object in three dimensions. Although drawing curves and surfaces in three dimensions by hand is more like an art, but it helps us to get better understanding about dimensions and surface areas. It eases solving the more complex math problems and calculations. I am interested in this class because I enjoy the challenging aspect of drawing three-dimensional objects on two-dimensional papers. This skill will be beneficial for my future career as a mathematician because it will enable me to calculate surface areas of various objects like a car or an airplane...etc..
The type of surfaces in the space are:

S

1.      Spheres: a sphere with center at (x₀, y₀, z₀) and radius r is defined to be the set of all points (x, y, z) such that the distance between (x, y, z) is r.

 

2.      Planes: the plan containing the point (x₁, y₁, z₁) and having normal vector n = (a, b, c) can be represented by the standard form of the equation of a plane.

 

 

3. Cylinder: the equation of a cylinder whose rulings are parallel to one of the coordinate axes contains only the variables corresponding to the other two axes.

 

 

4. Quadric surfaces: the equation of a quadric surface in space is a second- degree equation in three variables.

There are six basic types of quadric surfaces:

a.       Ellipsoid:

b. Hyperboloid of one sheet:

 

 

 

 

c.       Hyperboloid of two sheets:

 

d.       Elliptic cone:

 

e.       Elliptic paraboloid:

 

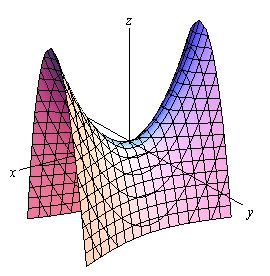
a.       Hyperbolic paraboloid: